{Musicians familiar with modes and scale harmonisation can skip to Part 2 of these pages}
It can be quite difficult to see complex relationships in chords and scales for hobby musicians who don’t deal with such things day in and day out. Aspects such as modes and enharmonic naming of chords tend to exacerbate this.
This topic discusses how both chords and scales can be coded, such that comparisons and relationships between them become logical and consistent using simple high school arithmetic. As other pages will show this also has some bearing on understanding and using features in Scaler such as the exported ‘state file’.
To start with, here is a reminder of some basics about scales. A ‘diatonic scale’ is a 7 note (heptatonic) scale with intervals in ‘tones’ and ‘semi-tones’ between the notes of T T S T T T S where T is a tone (or whole step) and S is a semi-tone (or half step). {some books do not use this definition, but this will be used here.} So in the case of a C major scale the notes are the white keys on a piano – C D E F G A B and then C again. The diagram below shows black keys between C an D and D and E; these are ‘whole steps’ or ‘tones’, being the T T in the as above formula. There is no black key between E and F and this is a ‘half step’ or ‘semi-tone’, and the S the formula.
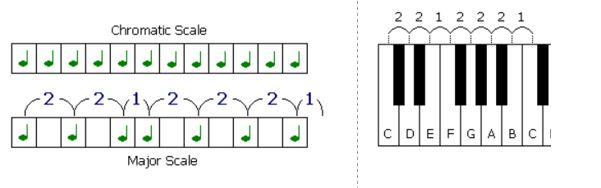
The C major scale (or often the ‘Ionian mode’) starts on C and uses he intervals above to describe the scale, giving the notes of C D E F G A B {C} . If instead we start on the note D (called the ‘second degree’) , and count off those intervals, the ‘scale’ becomes D E F G A B C {D}; this is what is termed a ‘mode of the major scale’, in this case the D Dorian mode of the diatonic major scale. The sequence for Dorian starts ‘TS’, and this means that the third note is a ‘minor third’, and so will produce a minor sound. It’s important to recognise the notes are exactly the same as in the C major scale. So for a 7 note scale, there are 7 modes, each built by applying the scale intervals to each note of the root scale in turn. Al the modes will have the same notes as the root scale.
If that is repeated starting with E, the sequence is E F G A B C D {E}, which is called the Phrygian mode. The intervals have now moved round to S T T T S T T. The sequence ‘ST’ is a minor second, and which occurs only in the Phrygian and Locrian modes. The latter is rarely used in ‘popular’ music, except maybe by bands such as Slipknot. (“Spiders”). [It would be true to say that this is a band with a perhaps limited following…]
It’s now possible to see that these modes are defined by ‘rotating’ each note of a scale to the left, and the moving the first note to the last position. This process is very familiar to computer folk as a common operation, but this view of things is not normally emphasized in standard music texts.
[Looking forward for a moment, if the question is asked “what notes to the Gb Lydian modes have in common with the E Locrian mode?”, a pencil and paper would probably be needed. But because we can assign a unique number to all chords and scales, we can easily tell this with some simple arithmetic. This can have a number of useful applications, as discussed in subsequent parts of this topic – bit that will come later. ]
Moving to chords related to a scale, one can form an associated chord by taking the 1st 3rd and 5th notes of the scale, and these three notes are together called a ‘triad’. So in the case of C major, the triad built in C is C, E and G; a C major triad. We can also create a triad out of the same notes, but starting the pattern on D, and we’ll get D, F and A. However, whereas the intervals were 2 tones between C and E, starting on D there are 3 semi-tones between D and F. This can be seen, as described above, as a ‘minor third, and the chord – D minor – will have a minor sound.
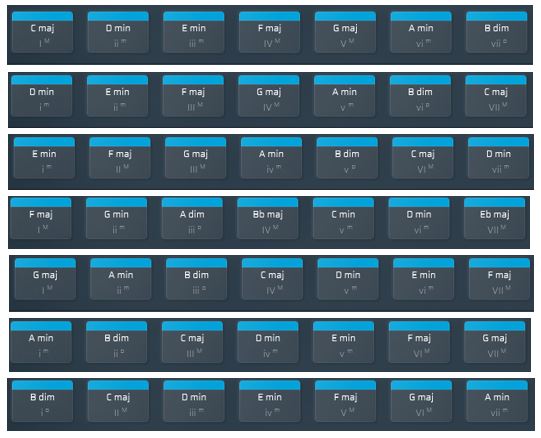
Building triads in this way is called the ‘harmonisation of the scale’ and to understand how chords will sound, it’s essential to get your head round this. Together with a grasp of modes, it a key element to advancing knowledge of music theory. However, there are some easy rules to recall this; remember the phrase “major, minor, minor, major, major. minor, diminished‘ for the harmonisation of the root of a major scale. So the harmonised triads built in C major are C major, D minor, E minor, F major, G major, A minor, and B diminished.
The notion of rotation applies here, so for the mode starting on the second note – Dorian – the phrase would be minor, minor, major, major, minor, diminished, major, i.e. D min, E mon, F maj, G maj, A min, B dim, C maj.
But “hold on” you say ” these are all the chords I write my pop songs with in the key of C”. Exactly, which is why understanding harmonisation is so important.
The harmonised chords is what section B in Scaler shows by default, so hopefully, if you were not aware of the process, you will now see how they arise.
Below shows the harmonisation of all 7 modes being named Ionian i.e. major, Dorian, Phrygian, Lydian, Mixolydian, Aeolian and Locrian. (see PS at bottom)
So the rules for all four types of triads (Major, Minor, Augmented and Diminished) as as follows, where a major third (‘M3’) has 4 semi-tones (‘TT’) and a minor third (‘m3’) has three semi-tones ( ‘TS’)
Major M3 + m3
Minor m3 + M3
Augmented M3 + M3
Diminished m3 + m3
Finally, be aware that the diatonic (7 note, with intervals TTSTTTS) is only one of many scales, which may have a varying number of notes and different intervals. So, for example. the 7 note ‘Melodic Minor’ root mode has intervals of TSTTTTS.
Ok., you should now have the necessary background on modes and their relationship to scales and harmonisation; now for Part 2 !
PS: What has been described here is the so call ‘derivative’ approach to understanding modes. There are other approaches,, but the main one is the ‘parallel’ approach. Here one takes a root (say, C), and then examines the difference between modes with the same root i.e. C major, C Dorian, C Phrygian and so on. So often a guitarist might follow this method and remember that a C Lydian mode was a major scale with a raised 4th note. This makes sense for a performing musician, but if you are using Scaler to compose by ear, it might be argued that ‘derivative’ is easier than ‘parallel’.